"Insulating and metallic phases in the one-dimensional Hubbard-Su-Schrieffer-Heeger model: Insights from a backflow-inspired variational wave function"
Davide Piccioni, Francesco Ferrari, Michele Fabrizio, Federico Becca
Phys. Rev. B 111, 045125 (2025)
The interplay between electron-electron and electron-phonon interactions is
studied in a one-dimensional lattice model, by means of a variational Monte
Carlo method based on generalized Jastrow-Slater wave functions. Here, the
fermionic part is constructed by a pair-product state, which explicitly depends
on the phonon configuration, thus including the electron-phonon coupling in a
backflow-inspired way. We report the results for the Hubbard model in presence
of the Su-Schrieffer-Heeger coupling to optical phonons, both at half-filling
and upon hole doping. At half-filling, the ground state is either a
translationally invariant Mott insulator, with gapless spin excitations, or a
Peierls insulator, which breaks translations and has fully gapped excitations.
Away from half-filling, the charge gap closes in both Mott and Peierls
insulators, turning the former into a conventional Luttinger liquid (gapless in
all excitation channels). The latter, instead, retains a finite spin gap that
closes only above a threshold value of the doping. Even though consistent with
the general theory of interacting electrons in one dimension, the existence of
such a phase (with gapless charge but gapped spin excitations) has never been
demonstrated in a model with repulsive interaction and with only two Fermi
points. Since the spin-gapped metal represents the one-dimensional counterpart
of a superconductor, our results furnish evidence that a true off-diagonal
long-range order may exist in the two-dimensional case.
"Monopole excitations in the $U(1)$ Dirac spin liquid on the triangular lattice"
Sasank Budaraju, Alberto Parola, Yasir Iqbal, Federico Becca, Didier Poilblanc
Phys. Rev. B 111, 125150 (2025)
The $U(1)$ Dirac spin liquid might realize an exotic phase of matter whose
low-energy properties are described by quantum electrodynamics in $2+1$
dimensions, where gapless modes exists but spinons and gauge fields are
strongly coupled. Its existence has been proposed in frustrated Heisenberg
models in presence of frustrating super-exchange interactions, by the
(Abrikosov) fermionic representation of the spin operators [X.-G. Wen,
\href{https://doi.org/10.1103/PhysRevB.65.165113}{Phys. Rev. B {\bf 65}, 165113
(2002)}], supplemented by the Gutzwiller projection. Here, we construct
charge-$Q$ monopole excitations in the Heisenberg model on the triangular
lattice with nearest- ($J_1$) and next-neighbor ($J_2$) couplings. In the
highly frustrated regime, singlet and triplet monopoles with $Q=1$ become
gapless in the thermodynamic limit; in addition, the energies for generic $Q$
agree with field-theoretical predictions, obtained for a large number of
gapless fermion modes. Finally, we consider localized gauge excitations, in
which magnetic $\pi$-fluxes are concentrated in the triangular plaquettes (in
analogy with $\mathbb{Z}_2$ visons), showing that these kind of states do not
play a relevant role at low energies. All our findings lend support to a stable
$U(1)$ Dirac spin liquid in the $J_1-J_2$ Heisenberg model on the triangular
lattice.
-
We reassess the modeling of amorphous silica bilayers as a two-dimensional
classical system whose particles interact with an effective pairwise potential.
We show that it is possible to reparameterize the potential developed by Roy,
Heyde, and Heuer to quantitatively match the structural details of the
experimental samples. We then study the glassy dynamics of the reparameterized
model at low temperatures. Using appropriate cage-relative correlation
functions, which suppress the effect of Mermin-Wagner fluctuations, we
highlight the presence of two well-defined Arrhenius regimes separated by a
narrow crossover region, which we connect to the thermodynamic anomalies and
the changes in the local structure. We find that the bond-orientational order
grows steadily below the crossover temperature and is associated to transient
crystalline domains of nanometric size. These findings raise fundamental
questions about the nature of glass structure in two dimensions and provide
guidelines to interpret the experimental data.
-
We clarify the relationship between freezing, melting, and the onset of
glassy dynamics in a prototypical glass-forming mixture model. Our starting
point is a precise operational definition of the onset of glassiness, as
expressed by the emergence of inflections in time-dependent correlation
functions. By scanning the temperature-composition phase diagram of the
mixture, we find a disconnect between the onset of glassiness and freezing.
Surprisingly, however, the onset temperature closely tracks the melting line,
along which the excess entropy is approximately constant. At fixed composition,
all characteristic temperatures display nonetheless similar pressure
dependencies, which are very well predicted by the isomorph theory. While our
results rule out a general connection between thermodynamic metastability and
glassiness, they call for a reassessment of the role of crystalline precursors
in glass-forming liquids.
"Roadmap on machine learning glassy dynamics"
Gerhard Jung, Rinske M. Alkemade, Victor Bapst, Daniele Coslovich, Laura Filion et al.
Nat. Rev. Phys. 7, 91 (2025)
Unraveling the connections between microscopic structure, emergent physical
properties, and slow dynamics has long been a challenge when studying the glass
transition. The absence of clear visible structural order in amorphous
configurations complicates the identification of the key physical mechanisms
underpinning slow dynamics. The difficulty in sampling equilibrated
configurations at low temperatures hampers thorough numerical and theoretical
investigations. This perspective article explores the potential of machine
learning (ML) techniques to face these challenges, building on the algorithms
that have revolutionized computer vision and image recognition. We present
recent successful ML applications, as well as many open problems for the
future, such as transferability and interpretability of ML approaches. We
highlight new ideas and directions in which ML could provide breakthroughs to
better understand the fundamental mechanisms at play in glass-forming liquids.
To foster a collaborative community effort, this article also introduces the
``GlassBench" dataset, providing simulation data and benchmarks for both
two-dimensional and three-dimensional glass-formers. We propose critical
metrics to compare the performance of emerging ML methodologies, in line with
benchmarking practices in image and text recognition. The goal of this roadmap
is to provide guidelines for the development of ML techniques in systems
displaying slow dynamics, while inspiring new directions to improve our
theoretical understanding of glassy liquids.
"Spin-phonon interactions on the kagome lattice: Dirac spin liquid versus valence-bond solids"
Francesco Ferrari, Federico Becca, Roser Valenti
Phys. Rev. B 109, 165133 (2024)
We investigate the impact of the spin-phonon coupling on the S=1/2 Heisenberg
model on the kagome lattice. For the pure spin model, there is increasing
evidence that the low-energy properties can be correctly described by a Dirac
spin liquid, in which spinons with a conical dispersion are coupled to emergent
gauge fields. Within this scenario, the ground-state wave function is well
approximated by a Gutzwiller-projected fermionic state [Y. Ran, M. Hermele,
P.A. Lee, and X.-G. Wen, Phys. Rev. Lett. 98, 117205 (2007)]. However, the
existence of U(1) gauge fields may naturally lead to instabilities when small
perturbations are included. Since phonons are ubiquitous in real materials,
they may play a relevant role in the determination of the actual physical
properties of the kagome antiferromagnet. We perform a step forward in this
direction, including phonon degrees of freedom (at the quantum level) and
applying a variational approach based upon Gutzwiller-projected fermionic
Ans\"atze. Our results suggest that the Dirac spin liquid is stable for small
spin-phonon couplings, while valence-bond solids are obtained at large
couplings. Even though different distortions can be induced by the spin-phonon
interaction, the general aspect is that the energy is lowered by maximizing the
density of perfect hexagons in the dimerization pattern.
"A simple linear algebra identity to optimize Large-Scale Neural Network Quantum States"
Riccardo Rende, Luciano Loris Viteritti, Lorenzo Bardone, Federico Becca, Sebastian Goldt
Communications Physics 7, 260 (2024)
Neural-network architectures have been increasingly used to represent quantum
many-body wave functions. These networks require a large number of variational
parameters and are challenging to optimize using traditional methods, as
gradient descent. Stochastic Reconfiguration (SR) has been effective with a
limited number of parameters, but becomes impractical beyond a few thousand
parameters. Here, we leverage a simple linear algebra identity to show that SR
can be employed even in the deep learning scenario. We demonstrate the
effectiveness of our method by optimizing a Deep Transformer architecture with
$3 \times 10^5$ parameters, achieving state-of-the-art ground-state energy in
the $J_1$-$J_2$ Heisenberg model at $J_2/J_1=0.5$ on the $10\times10$ square
lattice, a challenging benchmark in highly-frustrated magnetism. This work
marks a significant step forward in the scalability and efficiency of SR for
Neural-Network Quantum States, making them a promising method to investigate
unknown quantum phases of matter, where other methods struggle.
-
Recent progress in the design and optimization of neural-network quantum
states (NQSs) has made them an effective method to investigate ground-state
properties of quantum many-body systems. In contrast to the standard approach
of training a separate NQS from scratch at every point of the phase diagram, we
demonstrate that the optimization of a NQS at a highly expressive point of the
phase diagram (i.e., close to a phase transition) yields features that can be
reused to accurately describe a wide region across the transition. We
demonstrate the feasibility of our approach on different systems in one and two
dimensions by initially pretraining a NQS at a given point of the phase
diagram, followed by fine-tuning only the output layer for all other points.
Notably, the computational cost of the fine-tuning step is very low compared to
the pretraining stage. We argue that the reduced cost of this paradigm has
significant potential to advance the exploration of strongly-correlated systems
using NQS, mirroring the success of fine-tuning in machine learning and natural
language processing.
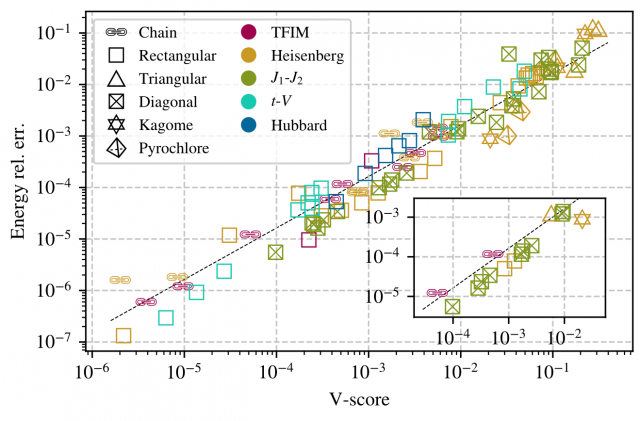
"Variational Benchmarks for Quantum Many-Body Problems"
Dian Wu, Riccardo Rossi, Filippo Vicentini, Nikita Astrakhantsev, Federico Becca et al.
Science 386, 296-301 (2024)
The continued development of computational approaches to many-body
ground-state problems in physics and chemistry calls for a consistent way to
assess its overall progress. In this work, we introduce a metric of variational
accuracy, the V-score, obtained from the variational energy and its variance.
We provide an extensive curated dataset of variational calculations of
many-body quantum systems, identifying cases where state-of-the-art numerical
approaches show limited accuracy, and future algorithms or computational
platforms, such as quantum computing, could provide improved accuracy. The
V-score can be used as a metric to assess the progress of quantum variational
methods toward a quantum advantage for ground-state problems, especially in
regimes where classical verifiability is impossible.
"Policy-guided Monte Carlo on general state spaces: Application to glass-forming mixtures"
Leonardo Galliano, Riccardo Rende, Daniele Coslovich
J. Chem. Phys. 161, 064503 (2024)
Policy-guided Monte Carlo is an adaptive method to simulate classical
interacting systems. It adjusts the proposal distribution of the
Metropolis-Hastings algorithm to maximize the sampling efficiency, using a
formalism inspired by reinforcement learning. In this work, we first extend the
policy-guided method to deal with a general state space, comprising, for
instance, both discrete and continuous degrees of freedom, and then apply it to
a few paradigmatic models of glass-forming mixtures. We assess the efficiency
of a set of physically inspired moves whose proposal distributions are
optimized through on-policy learning. Compared to conventional Monte Carlo
methods, the optimized proposals are two orders of magnitude faster for an
additive soft sphere mixture but yield a much more limited speed-up for the
well-studied Kob-Andersen model. We discuss the current limitations of the
method and suggest possible ways to improve it.
-
We study the quasiparticle properties of a dipolar impurity immersed in a
two-dimensional dipolar bath. We use the ab-initio Diffusion Monte Carlo
technique to determine the polaron energy, effective mass and quasiparticle
residue. We find that both the polaron energy and quasiparticle residue follow
a universal behaviour with respect to the polarization angle when properly
scaled in terms of the scattering length. This trend is maintained over a wide
range of values of the gas parameter, even in the highly correlated regime.
Instead, the effective mass shows growing anisotropy as the tilting angle is
increased, which is induced, mainly, by the anisotropy of the impurity-boson
dipole-dipole interaction. Surprisingly, the effective mass is larger in the
direction of minimum inter-particle repulsion. Finally, we use our Monte Carlo
results to check the accuracy of perturbative approaches and determine their
range of validity in terms of the gas parameter.
"Modified mean field ansatz for charged polarons in a Bose-Einstein condensate"
Ubaldo Cavazos Olivas, Luis A. Peña Ardila, Krzysztof Jachymski
Phys. Rev. A 110, L011301 (2024)
Ionic Bose polarons are quantum entities emerging from the interaction
between an ion and a Bose-Einstein condensate (BEC), featuring long-ranged
interactions that can compete with the gas healing length. This can result in
strong interparticle correlations and enhancement of gas density around the
ion. One possible approach to describe this complex system with high accuracy
relies on numerical treatment such as the quantum Monte Carlo (QMC) techniques.
Nevertheless, it is computationally very expensive and does not easily allow to
study the system dynamics. On the other hand, a mean-field based variational
ansatz in the co-moving frame can capture a sizeable change in the gas density.
We apply it to the case of regularized ion-atom potential and find that it
qualitatively reproduces the full numerical results. In addition, we also study
the system of two pinned ions, focusing on their effective interaction induced
by the bath. This approach seems to be promising for studying transport and
nonequilibrium dynamics of charged (bi)polarons in condensed media.
